Si estás buscando un artículo con ejemplos y ejercicios para sacar un buen resultado en el EvAU, este texto te proporcionará de manera práctica y sencilla sobre la distribución binomial. A continuación, aprenderás sobre un concepto fundamental en probabilidad y explicados en contextos específicos. Este blog abarca desde la definición y ejercicios de aplicaciones de la distribución binomial.
La distribución binomial es usada sobre experimentos que deben tener unas condiciones:
- El experimento debe repetirse en varias ocasiones.
- Los resultados del experimento deben ser éxito o fracaso.
- La probabilidad de éxito debe ser constante.
- Los ensayos deben ser independientes.

¿Qué es la distribución binomial?
La distribución binomial es un tipo de cálculo que nos dice cuántas veces puede pasar algo en una serie de pruebas que se hacen de la misma manera y que tienen la misma probabilidad de éxito o fracaso. Por ejemplo, si lanzamos una moneda 100 veces, la distribución binomial nos dice cuál es la probabilidad de obtener 50 caras y 50 sellos.

La distribución binomial está basado en un experimento de Bernoulli, que es cuando solo hay dos posibles resultados. A uno le llamamos "éxito" y tiene una probabilidad p de que ocurra, y al otro le llamamos "fracaso" y tiene una probabilidad 1-p de que ocurra. La distribución binomial tiene como principal uso el calculo del número de éxitos en una muestra de n elementos que se sacan con reemplazo de una población de N elementos.
Fórmula de distribución binomial
Denotamos el número de éxitos con la variable "x", como también llamamos a la variable "q" los. fracasis que son 1-p y representamos la distribución como b(x; n, p), obteniendo la siguiente formula:
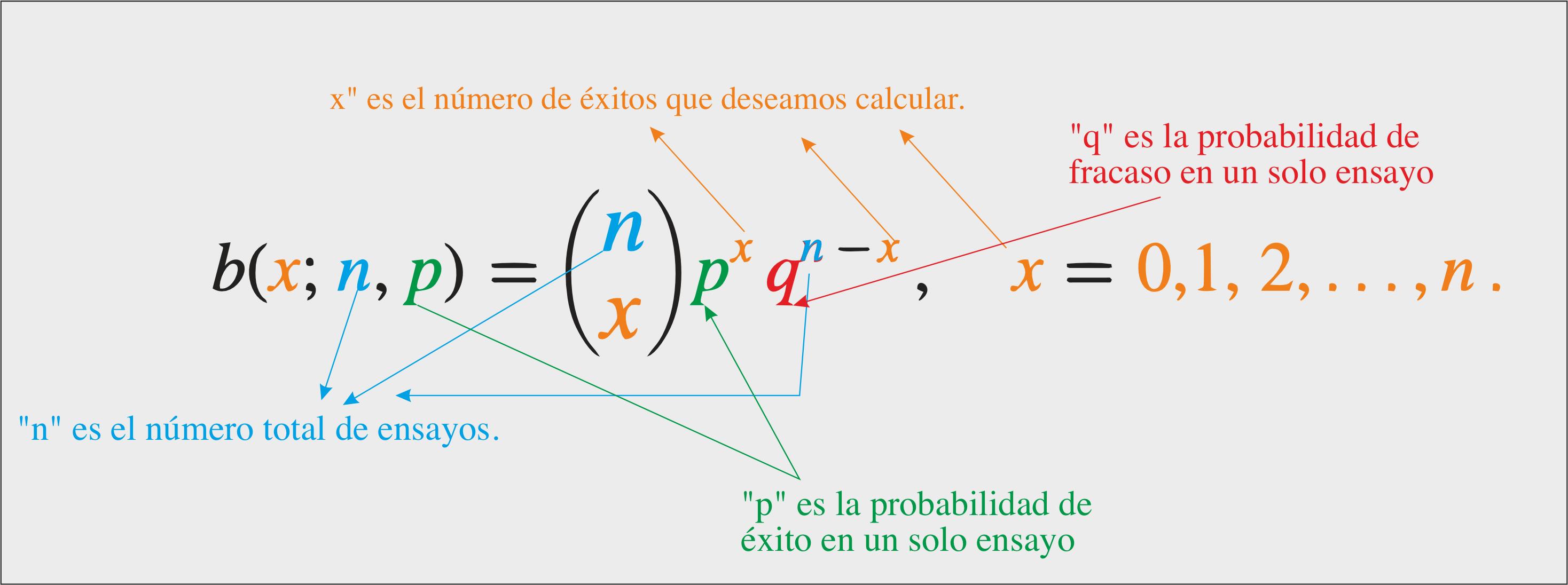
Además, la distribución binomial tiene como media y la varianza lo siguiente b (x; n, p) son:
![]()
Ejercicios prácticos matemáticos
1. En el distrito de Gracia de Barcelona se establece que el 75% de los robos ocurridos son producidos por extranjeros de no habla hispana. Calcule la probabilidad de que entre los siguientes cinco casos de robo que se reporten en este distrito.
a) Exactamente 2 sean producidos por extranjeros de países que su lengua no es castellano.
Para resolver este apartado, utilizaremos la distribución binomial, ya que estamos interesados en contar el número de éxitos (robos que comenten personas que no hablan español) en un número fijo de intentos (en nuestro ejercicio son cinco casos).

Como vemos, la probabilidad de que 2 de estos robos sean cometidos por personas que no hablan castellano es del 8.78% entre los 5 casos de robos registrados.
b) A lo sumo 3 sean producidos por extranjeros de que provienen de países que no hablan castellano.
Ahora, para hacer este apartado sumaremos las probabilidades de 0, 1, 2 y 3 robos, de la siguiente forma:
Primero lo calcularemos para P(x=0)
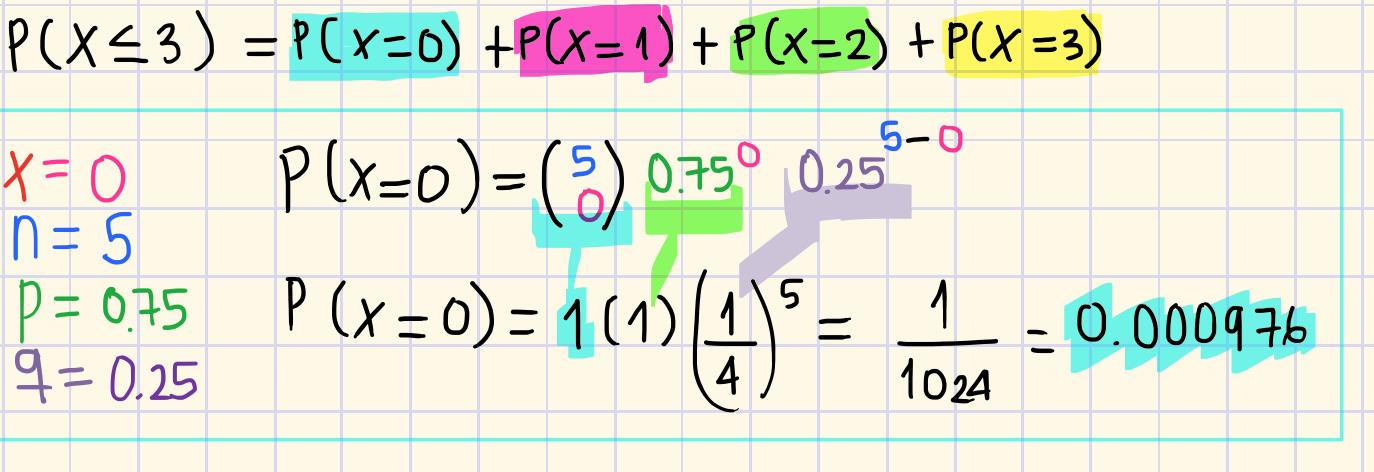
Realizaremos lo mismo, pero ahora para P(x=1)
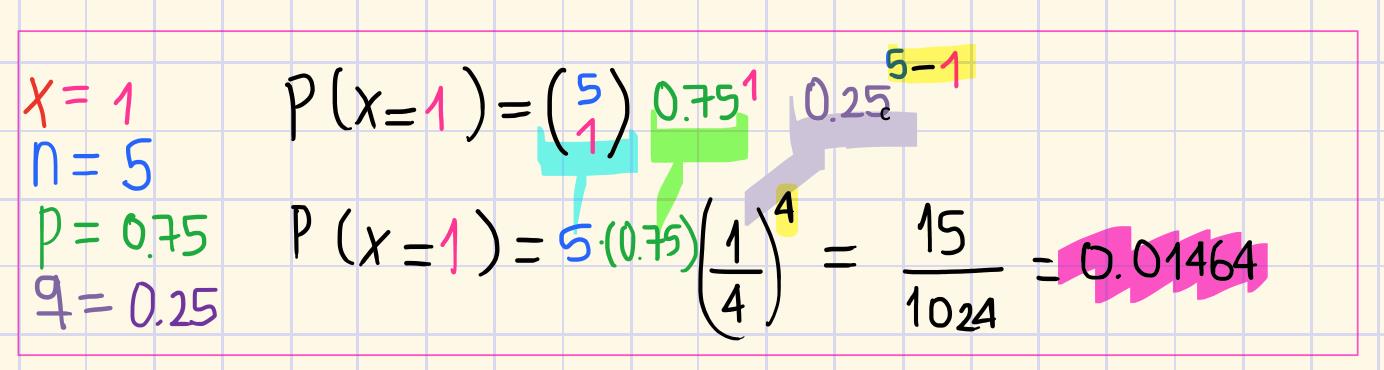
A continuación para P(x=2), en este aso usaremos lo realizado en el numeral "a" de este ejercicio:
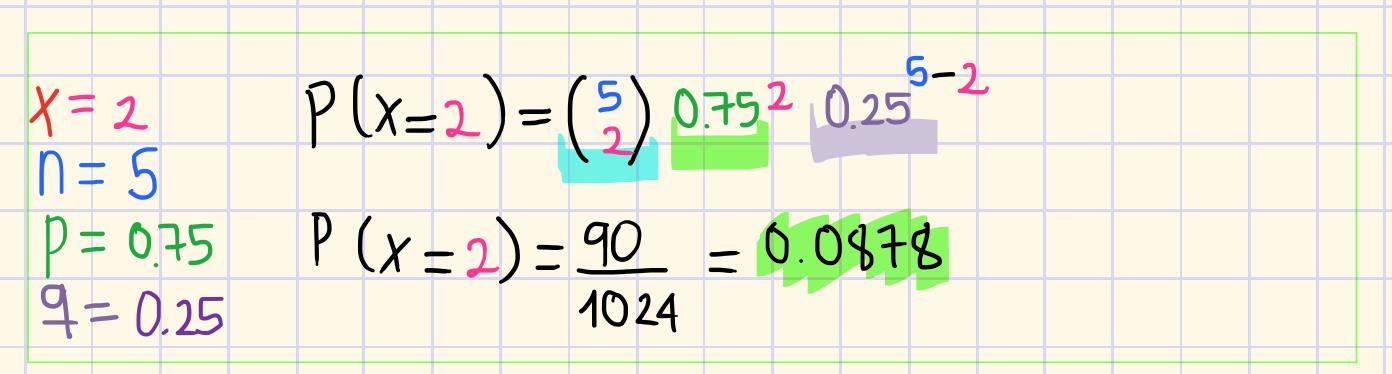
Y finalmente, para P(x=3)
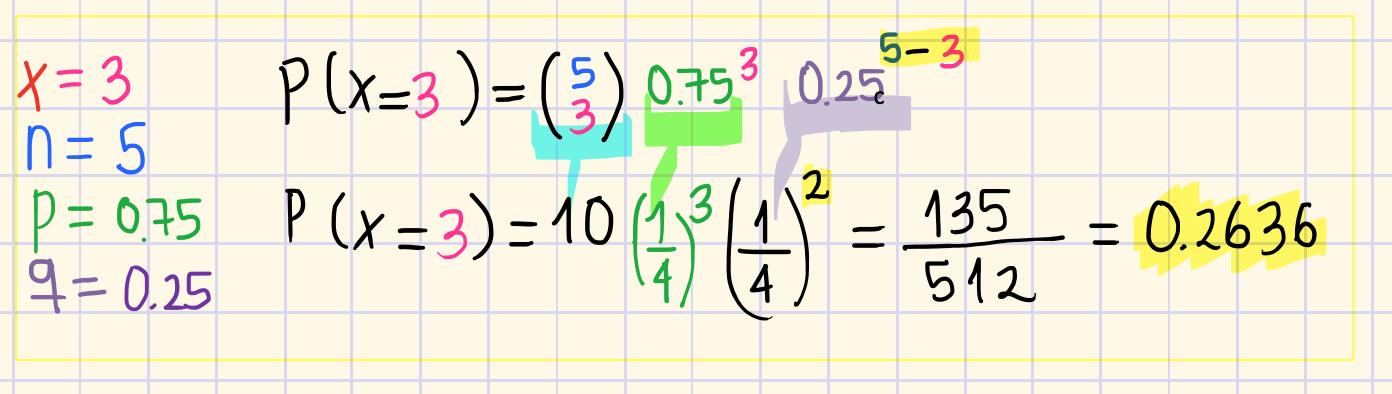
Como mencionamos debemos sumar todas las probabilidades que acabamos de calcular, están resaltadas. Así se vería todo el ejercicio:

Entonces terminamos sumando lo cual nos daría:
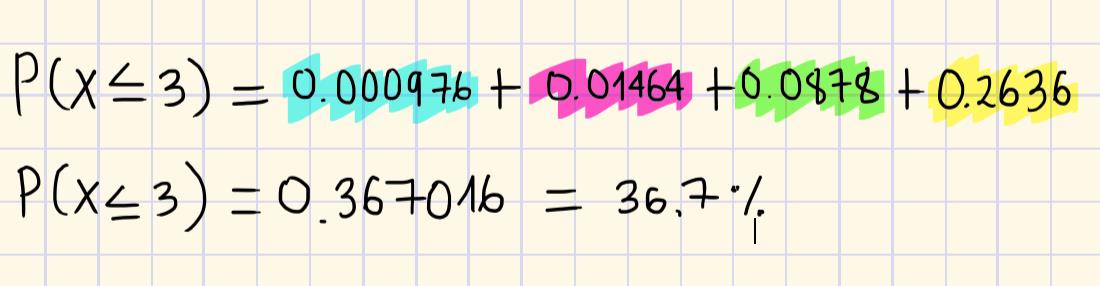
Por lo que, la probabilidad de 3 o menos robos sean cometidos por personas que no hablan castellano es del 36.7%.

