Las razones trigonométricas son razones entre los diferentes lados de un triángulo rectángulo. Aunque de primeras esto puede parecer difícil de comprender, una explicación más detallada, tal y como hago en mis clases de matemáticas, y algunos ejemplos, clarificarán el asunto rápidamente.
Debemos saber primeramente que las razones trigonométricas están relacionadas con los ángulos agudos (menores de 90º) de un triángulo rectángulo. Recordemos que un triángulo rectángulo es aquel que posee un ángulo recto, es decir, un ángulo de 90º. Las tres razones trigonométricas primarias son el seno (sen), el coseno (cos) y la tangente (tg). Definámoslas:

En estas fórmulas, alfa es el ángulo cuyas razones trigonométricas queremos calcular, pero, ¿qué son el cateto opuesto, el cateto contiguo y la hipotenusa?
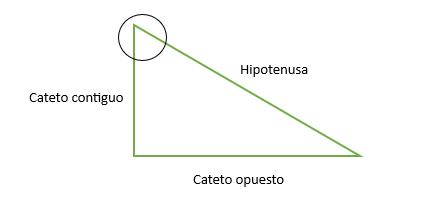
Todo triángulo rectángulo está formado por tres lados, el más largo se denomina hipotenusa, y los otros dos, catetos. Cuando estamos calculando las razones trigonométricas de un ángulo, el cateto contiguo será el que forma parte del ángulo, mientras que opuesto es aquel que está enfrentado al ángulo. Veámoslo con un ejemplo:
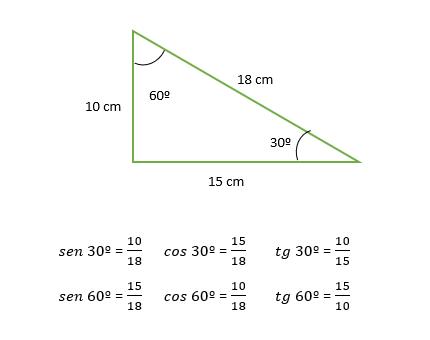
En la imagen se señala el cateto opuesto y el cateto contiguo con respecto al ángulo señalado. Démosle valores al ejemplo anterior:
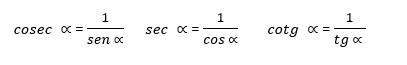
Debido a que la hipotenusa siempre es mayor que los catetos, tanto el seno como el coseno siempre tendrán un valor de entre 0 y 1 (ambos incluidos). De esta manera, la cosecante y la secante siempre serán iguales o mayores que 1.
Las otras tres razones trigonométricas, cosecante (cosec), secante (sec) y cotangente (cotg), se calculan a partir de las que ya hemos visto:

Relaciones trigonométricas fundamentales
Existen ciertas relaciones entre las razones trigonométricas que se denominan relaciones trigonométricas fundamentales, y son las siguientes:
DE CARA A LOS EJERCICIOS…
- Recuerda que si te dan solo dos de los lados del triángulo, puedes calcular el tercero utilizando el teorema de Pitágoras (h2 = c12 + c12), donde "h" es la hipotenusa, y "c1" y "c2" son los dos catetos
- Debes también saber que la suma de todos los ángulos de un triángulo rectángulo siempre es igual a 180º, así que si conoces dos de los ángulos, puedes calcular el tercero de ser necesario. Recuerda que en un triángulo rectángulo siempre existe un ángulo de 90º, por lo que es posible que este no te lo indiquen explícitamente al asumir que ya lo conoces.
- En las calculadoras existen las funciones “arcoseno”, “arcocoseno” y “arcotangente”, las cuales te permiten calcular un ángulo sabiendo sus razones trigonométricas. Por ejemplo, si se te proporciona el coseno de un ángulo, y a ti te interesa conocer a qué ángulo pertenece dicho coseno, deberás utilizar la función “arcocoseno” de la calculadora. De la misma manera, si tienes el seno de un ángulo y quieres averiguar el valor de dicho ángulo, debes utilizar la función "arcoseno" y, si te dan la tangente, la función "arcotangente". La forma de utilizar estas funciones varía dependiendo de la calculadora.
- Ø Un truco para no confundir las fórmulas del coseno y del seno es que en la del coseno aparece el cateto contiguo, ya que las dos palabras contienen las mismas dos primeras letras.

